2007-03-30 Ostatnia modyfikacja.
Zadanie
Zadanie.  Sprężyna.
Sprężyna.
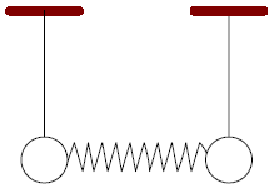
Dwa wahadła matematyczne o długości d i masie m każde połączono za pomocą słabej nieważkiej i nieodkształconej sprężyny o współczynniku sprężystości k (rys.1.). Znaleźć okres małych drgań w przypadkach:
a) każde wahadło odchylono o kąt ![]() w prawo od położenia
równowagi,
w prawo od położenia
równowagi,
b) pierwsze wahadło odchylono o kąt ![]() w prawo, drugie o kąt
w prawo, drugie o kąt ![]() w lewo od
położenia równowagi,
w lewo od
położenia równowagi,
c) odchylono tylko pierwsze wahadło o kąt ![]() w prawo od położenia
równowagi. Oblicz w tym punkcie również odstęp czasu, jaki upłynął pomiędzy chwilami czasu,
kiedy jedno wahadło przestaje drgać, a drugie wykazuje maksymalne drgania.
w prawo od położenia
równowagi. Oblicz w tym punkcie również odstęp czasu, jaki upłynął pomiędzy chwilami czasu,
kiedy jedno wahadło przestaje drgać, a drugie wykazuje maksymalne drgania.
Rozwiązanie
Dane:
Szukane
Rozwiązanie
Dla małych kątów suma momentów siły ciężkości i siły sprężystości względem osi obrotu dla lewego wahadła wynosi (rys.2.):
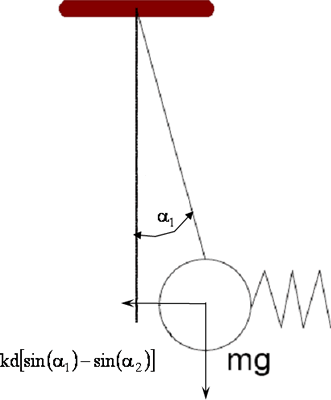
![]()
![]()
Stąd równanie ruchu obrotowego tego wahadła ma postać
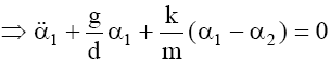
Podobnie otrzymamy dla drugiego wahadła i będziemy mieli układ równań
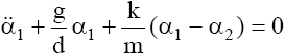 [1]
[1]
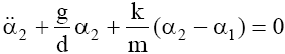 [2]
[2]
Oznaczając
![]()
![]()
oraz dodając lub odejmując stronami
równania (1) i (2) dostaniemy
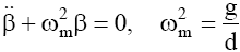 [3]
[3]
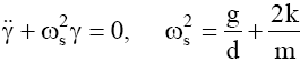 [4]
[4]
Widzimy
więc, że
![]()
i
![]()
spełniają równanie ruchu harmonicznego
prostego. Ogólne
rozwiązania
dla
![]()
i
![]()
można przedstawić w postaci
trygonometrycznej (patrz zadanie ze sprężyną)
![]() [5]
[5]
![]() [6]
[6]
Założenia
zadania sugerują następujące warunki początkowe:
![]()
![]()
![]()
![]()
Z równań (5), (6) i warunków początkowych mamy
![]() [7]
[7]
![]() [8]
[8]
Układ
równań (7) i (8) pozwala obliczyć ![]() i
i ![]()
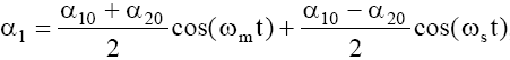 [9]
[9]
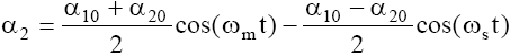 [10]
[10]
Dyskusja poszczególnych przypadków.
a) tu ![]() i
i ![]() , więc z [9] i [10] mamy
, więc z [9] i [10] mamy
![]()
Sprężyna
nie wpływa na ruch wahadeł matematycznych.
b) tu ![]() i
i ![]() , więc z [9] i [10] mamy
, więc z [9] i [10] mamy
![]()
![]()
Sprężyna
jest odkształcona, więc wpływa na ruch wahadeł, które drgają w przeciwfazie z częstością
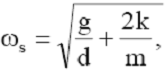
jednak
wpływ ten jest niewielki, ponieważ sprężyna jest słaba i częstość drgań wahadeł
jest bliska ![]()
c) tu ![]() i
i ![]() , więc z [9] i [10] mamy
, więc z [9] i [10] mamy
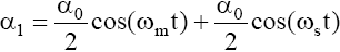 [11]
[11]
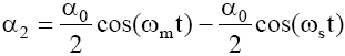 [12]
[12]
Mamy tu
do czynienia ze zjawiskiem dudnień, gdyż ![]() i
i ![]() niewiele się różnią od
niewiele się różnią od
siebie (sprężyna jest słaba), aby to uwidocznić wygodnie jest przedstawić równania (11) i (12)
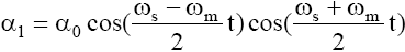 [13]
[13]
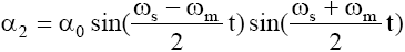 [14]
[14]
Częstość
![]() równanie (4) można
przedstawić w formie
równanie (4) można
przedstawić w formie
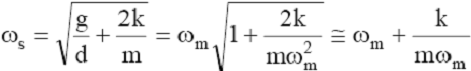
ponieważ
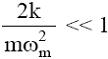
(sprężyna jest słaba),
wtedy równania (13) i (14) przyjmą postać
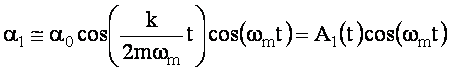 ,
, 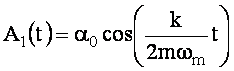
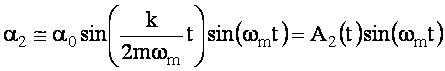 ,
, 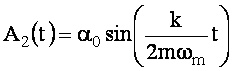
Moduły A1(t) i A2(t) są wolno zmiennymi w czasie amplitudami kątowymi odchyleń wahadeł od położenia równowagi. Okres dudnień Td określimy z równania
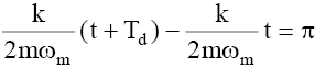
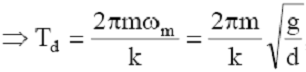
gdyż
okres funkcji |cos(x)|wynosi ![]() Odstęp czasu T12
pomiędzy maksymalnymi drganiami poszczególnych wahadeł wynosi
Odstęp czasu T12
pomiędzy maksymalnymi drganiami poszczególnych wahadeł wynosi
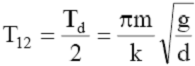
Odpowiedź
Odpowiedź
Dyskusja
Zadania z przedmiotu
Zadania