Zadanie

Zadanie. Sprężyna.

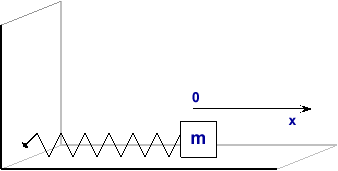
W układzie przedstawionym na rysunku masę m = 0,01 kg w chwili t = 0 s odchylono od położenia równowagi o x₀ = 0,01 m i nadano jej prędkość v₀ = 0,4 m/s.

Znaleźć zależność wychylenia, prędkości i przyspieszenia masy m od czasu.
Ile wynosi okres drgań, amplituda i faza początkowa wychylenia masy m?

Współczynnik sprężystości nieważkiej sprężyny k = 10 N/m. Tarcie zaniedbać.

Rozwiązanie

Dane:

Szukane

Rozwiązanie

Równanie ruchu masy m ma postać:

                  [1]

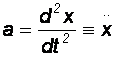
Porządkując równanie [1] otrzymamy równanie ruchu harmonicznego prostego
              [2]

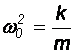
Szukamy nietrywialnego rozwiązania równania [2] w postaci
.
Obliczając drugą pochodną względem czasu z tak zapostulowanego rozwiązania i wstawiając do równania [2] otrzymamy:

  skąd mamy równanie charakterystyczne
                           [3]
Równanie [3] posiada dwa pierwiastki:
         
oraz    
      
gdzie  

Tak, więc równanie [2] ma dwa liniowo niezależne rozwiązania:
 

gdzie C₁ i C₂ są stałymi. Rozwiązanie ogólne równania [2] jest kombinacją liniową tych rozwiązań

            [4]

Równanie [4] zazwyczaj przedstawia się w postaci trygonometrycznej korzystając z wzorów Eulera

gdzie

Stałe A i B znajdujemy z warunków początkowych:

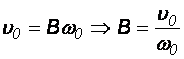
Zależność wychylenia masy m od czasu przedstawia się, więc następująco:

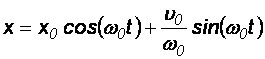                     [5]

Równanie [5] można przedstawić w postaci np. kosinusowej

                                    [6]

gdzie  

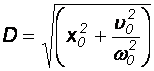
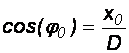
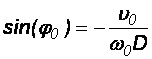
lub

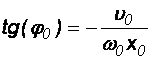
co łatwo pokazać przez sprawdzenie.

Na podstawie równań [6] uzyskamy

Okres drgań wynosi

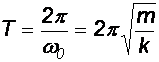
i po wstawieniu danych liczbowych T = 0,2 s.
Na podstawie równań [6] otrzymamy zależność prędkości v i przyspieszenia a masy m od czasu

a więc

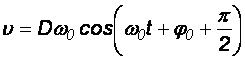
Odpowiedź

Odpowiedź

Dyskusja

 

Podstawa teoretyczna

Artykuły na stronie

Ruch drgający i falowy

Linki

...

Zadania z przedmiotu

Zadania