Zadanie

Zadanie. Wahadło w windzie.

Zadanie i rozwiązanie pochodzi ze strony Fizyka Jamnika

Jakim wzorem będzie wyrażał się okres drgań wahadła matematycznego o długości l
a) w windzie poruszającej się ze stałą prędkością,
b) w windzie poruszającej się w górę ze stałym przyspieszeniem a,
c) w windzie poruszającej się w dół ze stałym przyspieszeniem a,
d) w windzie spadającej swobodnie?

Rozwiązanie

Dane:

l - długość wahadła

Okres drgań wahadła matematycznego:

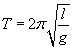
Siła bezwładności:

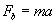
II zasada dynamiki Newtona:

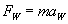
Szukane

T = ?

Rozwiązanie

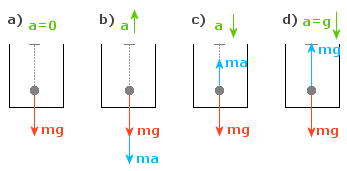
a)
Winda porusza się ze stałą prędkością. Oznacza to, że nie posiada ona przyspieszenia, czyli a = 0. Wzór na okres zależy tylko od przyspieszenia (długość nici jest dana i wynosi zawsze l), a ponieważ ono się nie zmienia, to okres w tym przypadku wynosi

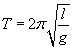
b)
Winda porusza się ze stałym przyspieszeniem a. Zakładamy, że przyspieszenie to jest mniejsze od przyspieszenia ziemskiego g. Jak to bywa w układach nieinercjalnych (nieinercjalny - ponieważ kulka znajduje się w poruszającej się windzie) pojawia się siła bezwładności, skierowana przeciwnie do zwrotu przyspieszenia (patrz rysunek). Wtedy wypadkowa siła wynosi

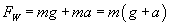
Wzór na okres drgań wahadła zapiszemy jako

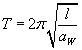
gdzie a_W oznacza przyspieszenie wypadkowe.
Zawsze pisaliśmy w tym wzorze wartość g bo uznawaliśmy, że na wahadło nie działa żadna inna siła poza siłą ciężkości. Teraz jednak jak widzimy dzieje się inaczej.
Z drugiej zasady dynamiki wiemy, że przyspieszenie wypadkowe to iloraz siły wypadkowej przez masę

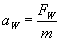
Stąd nasz okres wynosi:

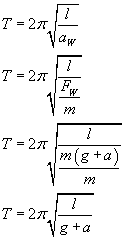
c)
Rozumowanie jest podobne jak w przypadku b).
Teraz przyspieszenie skierowane jest w drugą stronę, stąd siła wypadkowa będzie równa

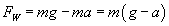
Stąd okres wynosi:

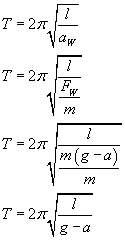
d)
A to jest przypadek czysto teoretyczny. Winda się urwała i spada swobodnie, czyli z przyspieszeniem ziemskim g. Czyli uwaga - siła ciężkości równoważy siłę wypadkową!

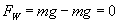
Stąd teraz okres wynosi

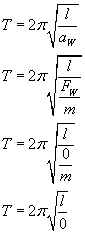
Jak to?! Przecież nie można dzielić przez zero! I to jest oczywiście prawda. To zero to wartość umowna. Wartość infinityzalna, czyli nieskończenie mała. Jak długość sznurka podzielimy przez wartość nieskończenie małą, otrzymamy wartość nieskończenie dużą. A pierwiastek z nieskończoności to oczywiście nieskończoność, nawet jak ją pomnożymy przez 2π. Stąd trzeba napisać, że

 

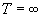
Odpowiedź

Odpowiedź

Dyskusja

 

Podstawa teoretyczna

Artykuły na stronie

Ruch drgający i falowy

Linki

...

Zadania z przedmiotu

Zadania