Zadanie

Zadanie. Rzut ukośny. Kompletne rozwiązanie

Z wysokości

wykonywany jest ukośnie do góry rzut pod kątem

do poziomu z szybkością

Wyznaczyć:

czas do momentu upadku
miejsce upadku
położenie końcowe
przemieszczenie całkowite
prędkość końcową
promień krzywizny w najwyższym punkcie toru
drogę całkowitą (odpowiedź można podać w formie całki oznaczonej)

 

Rozwiązanie

Dane

Szukane

Rozwiązanie

czas do momentu upadku
miejsce upadku
położenie końcowe
przemieszczenie całkowite
prędkość końcową
promień krzywizny w najwyższym punkcie toru
drogę całkowitą

 

Czas do momentu upadku.

Rys.1: Ilustracja przedstawia oznaczenia wysokości użyte w tekście.

Rzut ukośny jest złożeniem dwóch rzutów, rzutu pionowego do góry i ruchu jednostajnego (w kierunku poziomym). O czasie t lotu decyduje rzut pionowy (ciało porusza się do chwili spadnięcia na ziemię). W tym zadaniu obliczamy czas wznoszenia

wykorzystując znajomość przyspieszenia ziemskiego

Czas wznoszenia można obliczyć z następującego wyrażenia:

 (1)

gdzie

jest wysokością na jaką wzniesie się ciało liczoną od wysokości wystrzelenia ciała;

to składowa pionowa początkowej prędkości ciała.

Na wytłumaczenie zasługuje również minus we wzorze 1. Ciało wznosząc się traci prędkość, czyli hamuje. Hamowanie, zwane również opóźnieniem, to przyspieszenie ujemne. Oczywiście ciało spadające zwiększa swą prędkość i wtedy mamy przyspieszenie dodatnie, tak jak we wzorze 2

 (2)

Wzór 2 nie ma członu związanego z prędkością początkową z tego względu, że spadając z wysokości

(liczonej od poziomu 0) ma początkowo prędkość równą zeru.

Aby obliczyć całkowity czas ruchu t należy dodać do siebie czas wznoszenia

i czas spadania

 (3)

Z równania 1 możemy wyznaczyć
,
co daje:

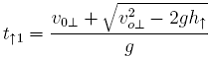 (4)

oraz

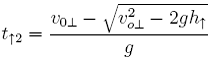 (5)

Oczywiście

możemy odrzucić ponieważ jest niefizyczny (czas nie może być mniejszy od zera).

Od tej pory zamiast

będziemy pisać po prostu
.
Nie znamy jeszcze wysokości

na jaką wzniesie się ciało.

Nie jest to żadnym problemem, ponieważ wykorzystując zasadę zachowania energii możemy napisać następujące równanie:

 (6)

W równaniu tym możemy zaniedbać tę część energii, która się nie zmienia w ciągu całego ruchu (energia kinetyczna związana z ruchem poziomym). Powyższe równanie zostało napisane przy założeniu, że energia potencjalna liczona jest od poziomu

.

Podczas wznoszenia się ciała energia kinetyczna maleje kosztem energii potencjalnej tak, że na wysokości maksymalnej

energia kinetyczna jest zerowa (pomijając energię ruchu poziomego) a energia potencjalna jest taka sama jak energia kinetyczna na wysokości

Można to napisać wprost:

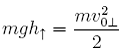 (7)

co prowadzi do rozwiązania

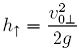 (8)

a to daje możliwość obliczenia czasu wznoszenia
.
Podstawiając 8 do 4 dostajemy czas wznoszenia.

 (9)

Teraz należy obliczyć czas spadania. W tym zadaniu nie jest on taki sam jak czas wznoszenia ponieważ wysokość z jakiej spada ciało jest inna od tej z jakiej zostało ono wystrzelone (patrz rys. 1).

Czas spadania można obliczyć przekształcając równanie 2 do postaci

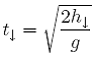 (10)

Jak można zauważyć z rysunku 1

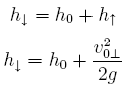 (12)

Po podstawieniu 12 do 10 zapisujemy

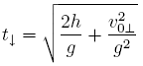 (13)

Czas ruchu zgodnie z 3 i po wykorzystaniu 9 oraz 13 można opisać wzorem

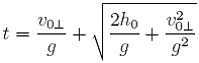 (14)

Zależność ta nie może być ostatecznym rozwiązaniem ponieważ nie mamy

danej wprost wartości . Składowe prędkości początkowej   są następujące:

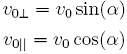(15) i (16)

Teraz podstawiając 15 do 14 otrzymujemy wreszcie ostateczne wyrażenie

pozwalające obliczyć całkowity czas ruchu.

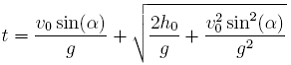 (17)

Po podstawieniu danych liczbowych uzyskujemy

Miejsce upadku.

Obliczenie miejsca upadku ciała z jest niezmiernie proste, gdy obliczyliśmy

już całkowity czas ruchu. Składowa pozioma prędkości v0II nie ulega zmianie

w ciągu całego ruchu (opór powietrza pomijamy). To właśnie ta składowa

decyduje o zasięgu rzutu ukośnego.

 (18)

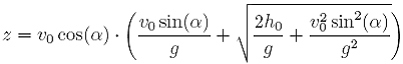 (19)

Co po podstawieniu danych daje

Położenie końcowe.

Zgodnie z rysunkiem 2 i równaniem ruchu w postaci parametrycznej, zapisanym

poniżej

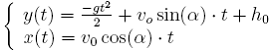 (20)

Otrzymujemy punkt położenia końcowego

o współrzędnych

czyli konkretnie

Przemieszczenie całkowite.

Przemieszczenie całkowite jest wektorem , mającym początek w punkcie

a koniec w punkcie

tak więc współrzędne tego wektora będą następujące

.

Długość wektora przesunięcia obliczamy

następująco

 (21)

Po podstawieniu danych współrzędne wektora przemieszczenia są następujące

 

oraz długość wektora przesunięcia

,

Prędkość końcowa.

Wektor prędkości końcowej tworzą dwie składowe.
Składowa równoległa do podłoża (jest ona równa składowej nie zmieniającej się w czasie ruchu).
Składowa prędkości

skierowana pionowo w dół rośnie z przyspieszeniem g, poczynając od zerowej prędkości na najwyższej wysokości do prędkości końcowej

tuż nad powierzchnią Ziemi. Składową v_kII można obliczyć np. z zasady zachowania energii, co prowadzi do równania

 (22)

Po prostych przekształceniach dostajemy

 (23)

Za podstawiamy wynik z (12)

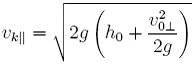 (24)

Można jeszcze podstawić wprost  z (15)

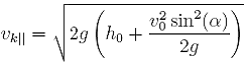 (25)

Nie wolno zapomnieć, że tak naprawdę celem naszym jest obliczenie prędkości końcowej, która jest wektorową sumą obydwu obliczonych wcześniej

składowych.

 (26)

Polecenie nie precyzuje czy należy podać jedynie długość wektora prędkości

końcowej czy także jego kierunek. Dlatego obliczmy i jedno i drugie.

Współrzędne wektora prędkości końcowej są już praktycznie obliczone.

Wystarczy zauważyć, że: składowe i

używane do tej pory, są wektorami równoległymi do osi obranego przez nas układu współrzędnych (patrz rys.2). Oznacza to, że (z dokładnością do znaku) są to współrzędne wektora prędkości końcowej , które ostatecznie zostały zapisane poniżej.

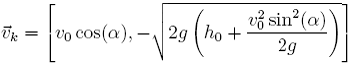 (27)

Liczbowe wartości są następujące

Mając współrzędne wektora prędkości można bez trudu obliczyć wartość

prędkości i po prostych przekształceniach otrzymamy

 (28)

i liczbowo

Promień krzywizny toru w najwyższym punkcie.

W najwyższym punkcie toru składowa prędkości styczna do toru jest równa

 

a przyspieszenie normalne do krzywizny toru to po prostu g. Tak więc promień okręgu stycznego do toru w najwyższym punkcie jest równy

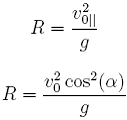(29) i (30)

Co po podstawieniu daje

Droga całkowita.

Aby obliczyć drogę przebytą wzdłuż krzywej należy wykonać całkowanie wzdłuż tej krzywej.
Kluczowe pytanie brzmi: jak to zrobić?

Należy podzielić krzywą na bardzo małe (infinityzymalne) odcinki dl. Aby obliczyć długość jakiegoś odcinka krzywej należy do siebie dodać wszystkie odcinki dl. Pojedynczy odcinek dl jest równy:

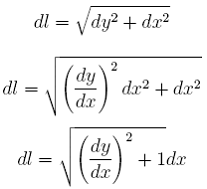
Teraz wystarczy wykonać sumowanie wszystkich odcinków dl, ale z racji, że odcinki dl są infinityzymalne, wykonujemy obustronne całkowanie dostając ogólny wzór na długość krzywej.

 (31)

Na podstawie parametrycznego równania ruchu (20) możemy wypisać równanie

opisujące kształt toru, gdzie nie występuje wprost parametr t (czas).

 (32)

Pochodna powyższej funkcji liczona po x ma następującą postać:

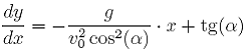 (33)

Podstawiając (33) do (31) dostajemy

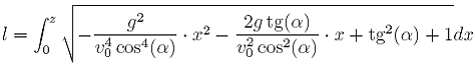 (34)

Granice całkowania obejmują całą odległość od miejsca wystrzelenia do miejsca

upadku (patrz rys. 2). Ze względu na dosyć rozbudowaną formułę opisującą górną granicę całki (patrz wzór 19) nie możliwe było wypisanie tej górnej granicy explicite.

Odpowiedź

Dyskusja

 

Podstawa teoretyczna

Artykuły na stronie

Rzuty

Linki

...

Zadania z przedmiotu

Zadania