Zadanie

Zadanie. Dynamika.

Na nitce o długości 50 cm zawieszono małą kulkę. Jaką najmniejszą prędkość należy nadać kulce w najniższym punkcie toru, by zakreśliła pełny obrót w płaszczyźnie pionowej?

Rozwiązanie

Dane

l = 50cm

Szukane

v = ?

Rozwiązanie

W zagadnieniu tym wygodnie jest posłużyć się nieinercjalnym układem odniesienia, w którym kulka spoczywa. Oznacza to, że działają na nią w każdym punkcie toru siły, których wypadkowa wynosi 0 N. Oczywiście musimy tu dodać siłę pozorną wynikającą z tego, że układ odniesienia porusza się z przyspieszeniem różnym od zera.

Podczas obrotu kulki w płaszczyźnie pionowej działa na nią siła ciężkości mg i siła ze strony nici F_N oraz wprowadzić musimy siłę pozorną zwaną siłą odśrodkową bezwładności F_odśr , ponieważ wybraliśmy opis w układzie nieinercjalnym.

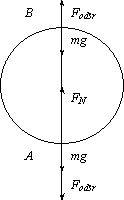
Rozpatrzmy siły działające na kulkę w najwyższym punkcie toru oznaczonym na rysunku przez B. Na kulkę działa siła ciężkości: mg oraz przeciwnie do niej skierowana siła odśrodkowa bezwładności. Jej wartość wynosi:

gdzie L jest długością nici.

Zastanówmy się jaka może być najmniejsza możliwa prędkość, przy której kulka pozostaje w ruchu na okręgu o promieniu L. Z analizy trzech wymienionych uprzednio sił wynika, że dla ruchu z najmniejszą możliwą prędkością, siła napięcia nici F_N znika i w układzie nieinercjalnym działają tylko siła ciężkości oraz siła odśrodkowa bezwładności. Jeśli prędkość zmniejszyłaby się jeszcze bardziej, wtedy kulka "spadnie" po torze o promieniu mniejszym niż długość nici L. Stąd w punkcie B w układzie nieinercjalnym związanym z kulką siła wypadkowa równa jest zeru (kulka w tym układzie spoczywa):

Stąd obliczamy prędkość minimalną w punkcie B:

Aby znaleźć związek minimalnej prędkości, którą trzeba nadać kulce, by zakreśliła pełny obrót z wygodnie jest wykorzystać potencjalność pola grawitacyjnego. Całkowita energia mechaniczna w tym ruchu jest zachowana. Wybierając położenie górne - B (oznaczone indeksem 1) oraz dolne - A (oznaczone indeksem 2) położenie kulki otrzymamy zależność:

W równaniu tym przyjęto dla wygody poziom odniesienia dla energii potencjalnej za zerowy w punkcie A na okręgu. Stąd energia potencjalna w punkcie B wynosi mg2L.

Wstawiając w to równanie wartość:

otrzymamy po prostych przekształceniach szukaną minimalną wartość prędkości:

Odpowiedź

Prędkość nadana cząstce wynosi
.

Dyskusja

 

Podstawa teoretyczna

Artykuły na stronie

Linki

...

Zadania z przedmiotu

Zadania