Zadanie

Zadanie. Częstotliwość fali światła. Kamil Jurowski.

Według teorii Bohra atom wodoru składa się z dodatnio naładowanego jądra (protonu) i krążącego wokół niego elektronu. Elektron taki w stanie podstawowym ma energię równą -13,6 eV.

Oblicz, jaką częstotliwość ma fala emitowana przez inny atom przy przejściu elektronu z orbity czwartej na trzecią. Wiedząc, że fala świetlna to fala elektromagnetyczna rozchodząca

się z prędkością światła
,
a stała Placka wynosi
.

Rozwiązanie

Dane

Szukane

T_j=?

Rozwiązanie

Aby obliczyć kwant energii światła należy skorzystać ze wzoru:

 gdzie:

h     - stała Plancka

   - częstotliwość fali,

Energia ta będzie równa różnicy energii jakie posiada elektron na poszczególnych orbitach

gdzie:

- energia elektronu na dalszej powłoce (dalej od jądra atomowego)

 - energia elektronu na bliższej powłoce (bliżej jądra atomowego)

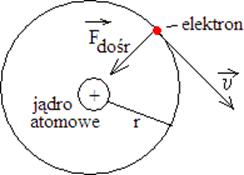
Schematyczny rysunek:

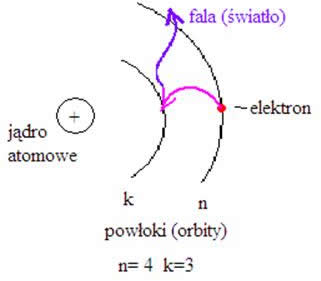
 (1.1)

Energia elektronu to energia kinetyczna + energia potencjalna:

                 

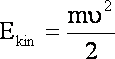
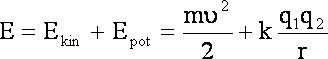
Ponieważ i po wstawieniu k do licznika stąd:

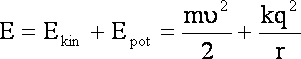
Wartość q dotyczy elektronu a wiec ładunku elementarnego e. Związku z tym, że założenia dotyczą elektronu, który ma ładunek ujemny, wartość członu określającego energię potencjalną będzie zawierał znak minus.

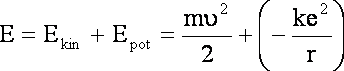  (1.2)

z kolej po porównaniu F dośrodkowej krążącego elektronu z jego siłą elektrostatyczną:

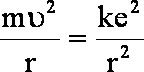
po podzieleniu obu stron przez r

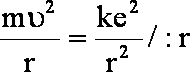
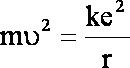 (1.3)

Wartości (1.3) do (1.2), otrzymujemy:

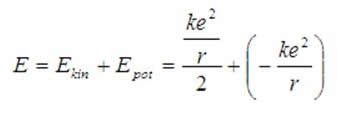
Po zmianie znaków:

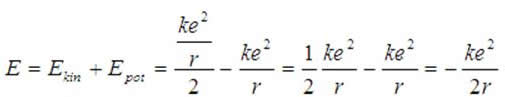
Otrzymujemy:

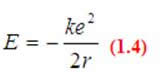
 Z pierwszego warunku Bohra:

,,Moment pędu elektronu musi być równy wielokrotności stałej Plancka przez ".

Co można zapisać:

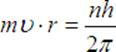
Po przekształceniu

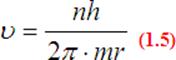
Po porównaniu siły dośrodkowej działającej na elektron i siły elektrostatycznej

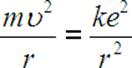
Po podstawieniu za v równania 1.5, otrzymujemy:

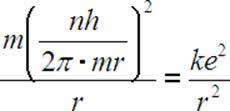
Po pomnożeniu na krzyż:

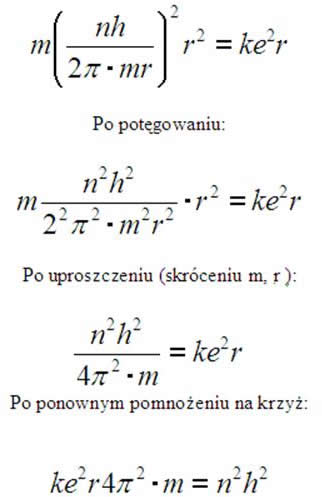
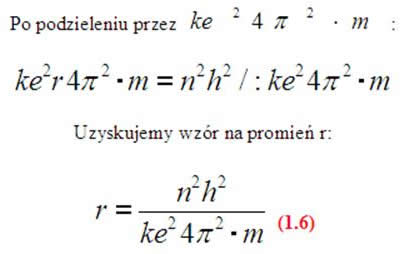
Łatwo zauważyć, że n to numer powłoki, jeżeli podstawilibyśmy liczbę 1, to uzyskalibyśmy wartość promienia atomu wodoru (ponieważ ma jedną orbitę- jeden krążący elektron wokół jądra).

Stąd wartość promienia atomu wodoru:

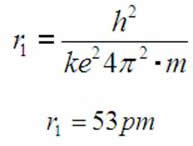
Podstawiając do wzoru (1.6) wartość:

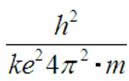
 jako    uzyskujemy:

 (1.7)

Podstawiając wzór (1.7) do wzoru (1.4)

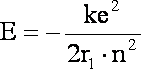
Ponownie łatwo zauważyć, że podstawiając ża n=1 uzyskamy tym razem wartość energii dla pierwszej orbity, stan podstawowy atomu wodoru, wiec można wyrażenie:

zastąpić symbolem

 

jako energia stanu podstawowego:

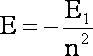  (1.8)

Po żmudnych, ale niezbędnych obliczeniach dotarliśmy do upragnionej wartości na energię elektronu na różnych orbitach, jednak to nie koniec naszej przygody z przekształceniami wzorów....

Wracając do naszego wzoru (1.1):

za

 

i za

podstawiamy wyrażenie (1.8) odpowiednio zmieniając oznaczenia energii dla poszczególnych orbit:

 

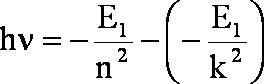
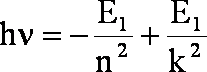
po wyciągnięciu E₁ przed nawias i uporządkowaniu wyrazów:

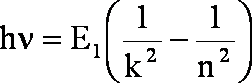
Po podzieleniu przez h:

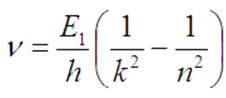(1.9)

Ponieważ

Po przekształceniu na :

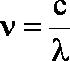 (1.10)

Po podstawieniu wzoru (1.10) do wzoru (1.9)

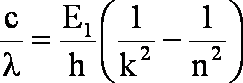
po podzieleniu przez c:

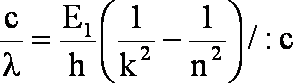
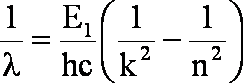
Warto wiedzieć, że wartość  to stała Rydberga

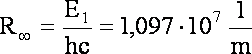
Po zastąpieniu tego członu stałą Rydberga uzyskujemy upragniony wzór Balmera:

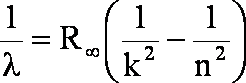
Stąd możemy obliczyć długość fali

Dane:

n = 4,

k = 3

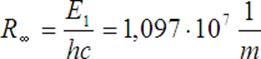
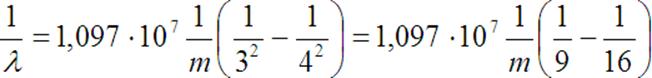
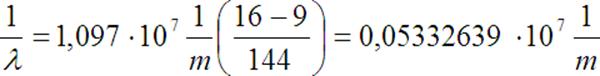
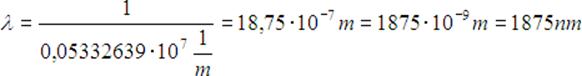
Korzystając znowu ze wzoru  (1.10)

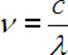
Wyliczamy częstotliwość

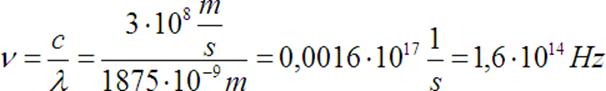
Odpowiedź

Częstotliwość fali światła pochodzącej z emisji atomu przy przejściu elektronu z orbity czwartej na trzecią wynosi
.

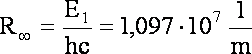Dyskusja

Podstawa teoretyczna

Artykuły na stronie

Linki

...

Zadania z przedmiotu

Zadania